 |
 |
|
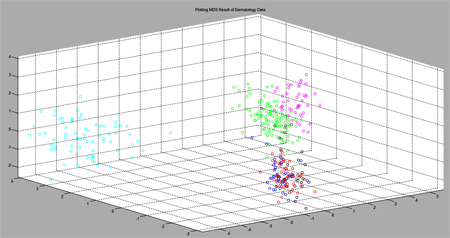
Figure 1 : An example plot of CFMDS result (drawn using MATLAB) |
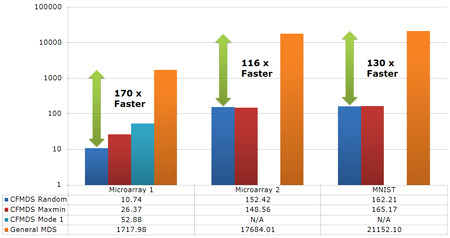
Figure 2 : Running time comparision of CFMDS and general MDS. (The vertical axis is in log-scale and the time unit is seconds.) |
 |
 |
|
Figure 1 : An example plot of CFMDS result (drawn using MATLAB) |
Figure 2 : Running time comparision of CFMDS and general MDS. (The vertical axis is in log-scale and the time unit is seconds.) |
| 1. Introduction |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Multidimensional scaling (MDS) is a widely used method for dimensionality reduction.
MDS has mainly been applied to data visualization and feature selection.
Among various MDS methods, the classical MDS is not quite appropriate for quick analysis of data having large numbers of objects, on normal desktop computers due to its computational complexity.
In precise, it usually takes several hours to project datasets consisting of tens of thousands of data points by the classical MDS.
We propose an efficient approximation algorithm for the classical MDS based on divide-and-conquer and CUDA. CUDA (Compute Unified Device Architecture, http://www.nvidia.com/object/cuda_home_new.html) is NVIDIA's parallel computing architecture exploiting the power of the GPU (graphics processing unit). The principle of divide-and-conquer is applied for circumventing the small memory problem of usual graphics cards. Our application software, i.e., CFMDS is an expeditious solution for analysis and visualization of data containing several thousands of objects, which is hundreds times faster than general MDS softwares. |
||||||||||||||||||||||||||||||||||||||||||||||||
| 2. CFMDS (CUDA-based Fast Multidimensional Scaling) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
CFMDS (CUDA-based Fast Multidimensional Scaling) is an implementaton of the classical MDS based on Euclidean distances between objects, using CUDA and divide-and-conquer.
CFMDS has two running modes : the classical MDS based on CUDA (Mode 1) and the approximate classical MDS based on divide-and-conquer for large data (Mode 2). If input data size is bigger than the maximum size of GPU's free memory, CFMDS uses a divide-and-conquer approach. The number and size of data partitions are automatically decided by the size of available memory. CFMDS with divide-and-conquer samples data points from each partition. Two ways of sampling are Random and Maxmin. Random denotes usual random sampling without replacement. In the Maxmin approach, data points are chosen one at a time, and each new point maximizes, over all unused data points, the minimum distance to any of the previously-sampled points. The Random approach works quite well in practice. Maxmin has the advantage of being controllable, which may be useful in some contexts where data manifold is skewed. If input data size is smaller than the maximum size of GPU's free memory, CFMDS apply the classical MDS algorithm. This mode is not based on divide-and-conquer and random sampling, so it produces the same results as the original classical MDS. |
||||||||||||||||||||||||||||||||||||||||||||||||
| 3. System Requirements |
||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
| 4. How to Use |
||||||||||||||||||||||||||||||||||||||||||||||||
|
All parameters has to be set when running the application. The input data file format should be n x n dissimilarity matrix (Tab delimited. Each row is separated by '\n'. See the sample data far below).
If input data includes header information, then the header information must be located on the first row and column.
Our applicaiton generates four output files, that is, result of MDS, indexes of sampled data points (for Mode 2), logs of CFMDS process, and eigenvalues (optional).
The format of each output files is based on column-major order. CFMDS has seven parameters which are described in Table 1.
|
||||||||||||||||||||||||||||||||||||||||||||||||
| 5. License |
||||||||||||||||||||||||||||||||||||||||||||||||
|
CFMDS is distributed under the GNU General Public License version 2. A copy of that license should be distributed with every copy of CFMDS or derivatives of CFMDS. For complete information about the GNU GPL please visit the Free Software Foundation. |
||||||||||||||||||||||||||||||||||||||||||||||||
| 6. Downloads |
||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
| 7. Contact Information |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Specific questions regarding the use of CFMDS may be sent to Kyu-Baek Hwang and Sungin Park. Bug reporting on CFMDS may be sent to Sungin Park. Questions about CUDA and CULA setting or compile for CFMDS may be sent to Sungin Park. General inquiries may be addressed to Kyu-Baek Hwang. |
||||||||||||||||||||||||||||||||||||||||||||||||